Recent mathematical proof of existence and uniqueness of the global minimum of cost functionals formulated by the Self-OPTIM framework for the case of anisotropic and elastic materials
M. Wolff, M. Böhm. Zu einem neuen Ansatz zur Parameterbestimmung in der Mechanik der Festkörper. Berichte aus der Technomathematik 13-03, Universität Bremen, 2013. (In German)
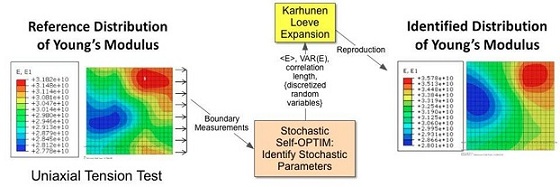
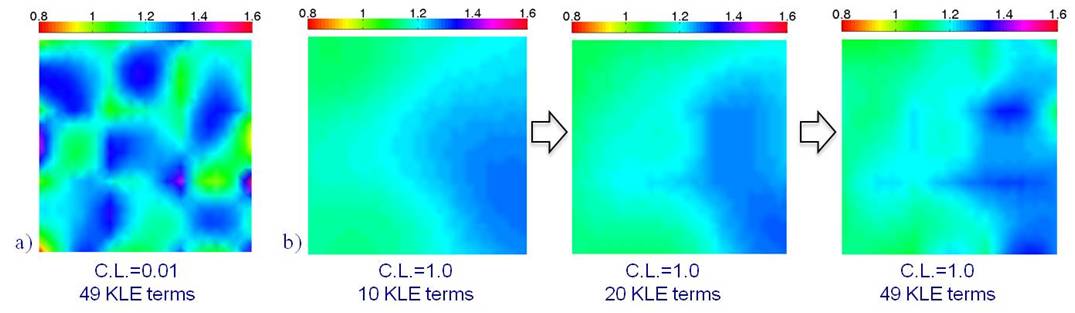
(a) Stochastic Self-OPTIM for Reconstruction of Material Properties With Spatial Randomness
(b) Modeling and Identification of Spatially Varying Random Field, Diffusivity in Concrete Materials
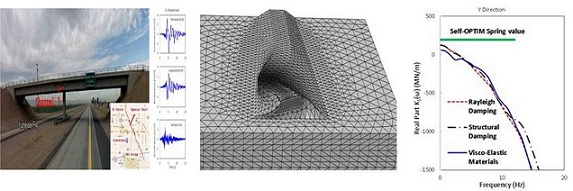
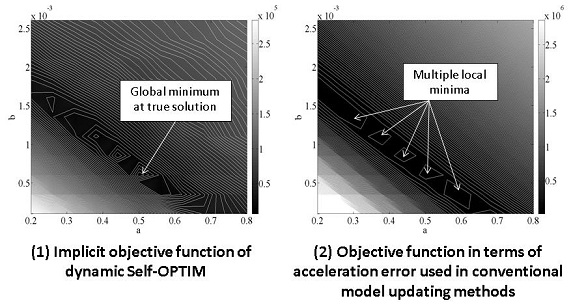(c) Advantage of Implicit Objective Function in Dynamic Self-OPTIM: Rayleigh Damping Identification of Three-Story Building Structure
(d) Damping Identification of Bridge Embankment Using Records (Dynamic Self-OPTIM)
Self-Optimizing Inverse Method (Self-OPTIM) can automatically determine model parameters related to constitutive and damage evolution laws, etc. from global structural response by minimizing an implicit error function in terms of stress-strain fields. Applications of the Self-OPTIM is quite broad including, but not limited to, material characterization, model parameter identification, model updating, and damage characterization in the field of computational and experimental mechanics and structural health monitoring, etc. For its generality, it can also be applied to many engineering boundary and initial valuae problems. Our group is undertaking research on applications and extentions of the Self-OPTIM to various inverse problems in engineering mechanics and structural health monitoring with considerations of uncertainties in physical material systems and measurement noise/errors. Expected outcomes of this research will significantly increase accuracy of computational simulations of complex material systems and structures.
<Patents filed>
G.J. Yun, & S. Shang, “Self-Optimizing Inverse Analysis Method for Parameter Identification of Nonlinear Material Constitutive Models,” Non-provisional filing, US13/748,905, 2013
G.J. Yun, “Method and Computer Program for Extracting Stochastic Information and Reconstructing Random Fields: Nonlinear Stochastic Self-OPTIM,” Provisional filing, USPTO: 61/869,907, 2013